Look at the amazing things going on in Mathematics at St Paulinus

Curriculum Intent:

How do we intend to achieve our curriculum vision in Mathematics lessons?

Mathematics is a creative and highly inter-connected discipline that has been developed over centuries, providing the solution to some of history’s most intriguing problems. It is essential to everyday life, critical to science, technology and engineering, and necessary for financial literacy and most forms of employment. A high-quality mathematics education therefore provides a foundation for understanding the world, the ability to reason mathematically, an appreciation of the beauty and power of mathematics, and a sense of enjoyment and curiosity about the subject. (DfE, 2013)

At St Paulinus, we follow the National Curriculum which aims to ensure that all pupils:

• become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately.
• reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language
• can solve problems by applying their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.

As mathematics is an interconnected subject, learners are required to fluently move between different representations of mathematical ideas. Although the programmes of study are organised into distinct units, pupils are given lots of opportunity to make rich, meaningful connections across mathematical ideas, so that they develop mathematical problem solving and reasoning skills. Links to other subjects are also explicitly highlighted within the mathematics curriculum. In using a mastery approach to the mathematics curriculum, the majority of children are expected to progress at broadly the same pace. However, decisions on when to progress are based on the security of their understanding. For learners who grasp a concept quickly, challenges are planned for which give them the opportunity to solve rich and sophisticated problems before accelerating through new content. Similarly, those learners who are not fully fluent with concepts have the opportunity to consolidate their understanding through targeted Do Now tasks (see subject policy), differentiated activities and/or daily intervention.

 

 

Long term plan – Nursery

 

 

Long term plan – Reception to Year 6

	Autumn Term	Spring Term	Summer Term
Reception	Talk about measure and patterns Circles and triangles Shapes with 4 sides ·         identify when a set can be subitised and when counting is needed ·         subitise different arrangements, both unstructured and structured, including using the Hungarian number frame ·         make different arrangements of numbers within 5 and talk about what they can see, to develop their conceptual subitising skills ·         spot smaller numbers ‘hiding’ inside larger numbers ·         connect quantities and numbers to finger patterns and explore different ways of representing numbers on their fingers ·         hear and join in with the counting sequence, and connect this to the ‘staircase’ pattern of the counting numbers, seeing that each number is made of one more than the previous number ·         develop counting skills and knowledge, including: that the last number in the count tells us ‘how many’ (cardinality); to be accurate in counting, each thing must be counted once and once only and in any order; the need for 1:1 correspondence; understanding that anything can be counted, including actions and sounds ·         compare sets of objects by matching ·         begin to develop the language of ‘whole’ when talking about objects which have parts	Mass and capacity Length, height and time Explore 3-D shapes ·         continue to develop their subitising skills for numbers within and beyond 5, and increasingly connect quantities to numerals ·         begin to identify missing parts for numbers within 5 ·         explore the structure of the numbers 6 and 7 as ‘5 and a bit’ and connect this to finger patterns and the Hungarian number frame ·         focus on equal and unequal groups when comparing numbers ·         understand that two equal groups can be called a ‘double’ and connect this to finger patterns ·         sort odd and even numbers according to their ‘shape’ ·         continue to develop their understanding of the counting sequence and link cardinality and ordinality through the ‘staircase’ pattern ·         order numbers and play track games ·         join in with verbal counts beyond 20, hearing the repeated pattern within the counting numbers	Manipulate, compose and decompose Sharing and grouping Visualise, build and map Make connections ·         continue to develop their counting skills, counting larger sets as well as counting actions and sounds ·         explore a range of representations of numbers, including the 10-frame, and see how doubles can be arranged in a 10-frame ·         compare quantities and numbers, including sets of objects which have different attributes ·         continue to develop a sense of magnitude, e.g. knowing that 8 is quite a lot more than 2, but 4 is only a little bit more than 2 ·         begin to generalise about ‘one more than’ and ‘one less than’ numbers within 10 ·         continue to identify when sets can be subitised and when counting is necessary ·         develop conceptual subitising skills including when using a rekenrek
Year 1	Place Value (within 10) Addition and Subtraction (within 10) Shape	Place Value (within 20) Addition and Subtraction (within 20) Place Value (within 50) Length and Height Mass and Volume	Multiplication and Division Fractions Position and Direction Place Value (within 100) Money Time
Year 2	Place Value Addition and Subtraction Shape	Money Multiplication and Division Length and Height Mass, Capacity and Temperature	Fractions Time Statistics Position and Direction
Year 3	Place Value Addition and Subtraction Multiplication and Division A	Multiplication and Division B Length and Perimeter Fractions A Mass and Capacity	Fractions B Money Time Shape Statistics
Year 4	Place Value Addition and Subtraction Area Multiplication and Division A	Multiplication and Division B Length and Perimeter Fractions Decimals A	Decimals B Money Time Shape Statistics Position and Direction
Year 5	Place Value Addition and Subtraction Multiplication and Division A Fractions A	Multiplication and Division B Fractions B Decimals and Percentages Perimeter and Area Statistics	Shape Position and Direction Decimals Negative Numbers Converting Units Volume
Year 6	Place Value Addition, Subtraction, Multiplication and Division Fractions A Fractions B Converting Units	Ratio Algebra Decimals Fractions, Decimals and Percentages Area, Perimeter and Volume Statistics	Shape Position and Direction Themed projects, consolidation and problem solving

 

Curriculum Implementation:

What does Mathematics teaching look like?

 At St Paulinus, children receive five maths lessons each week. As well as daily maths lessons, children take part in frequent ‘Maths Meetings’. These are short sessions aimed at consolidating previous knowledge and even pre-teaching upcoming units of work. They cover a variety of mathematical concepts (including those units which may only appear once per year group) so that learning is rarely forgotten and constantly utilised. All children are required to take part in Maths Meetings and do so through songs, quick-fire quizzes, the use of manipulatives or recording an answer on their whiteboard. Maths meetings are designed to be short, fun sessions that embed key concepts within the mathematics curriculum.

In Reception and Key Stage One, our pupils participate in the Mastering Number programme of work, which is a ten minute daily maths lesson. These sessions are designed to be engaging and an opportunity for every child to succeed. The sessions are focussed on the composition of number including subitising, patterns and number bonds.

Our daily lessons follow the structure of ‘I do, We do, You do’ to allow for gradual release and allowing children to increase their independence through supported practice.

In year groups that move between a carpet space and tables, Transition activities are used so that all lesson time is utilised. This is done through chanting number bonds, timetable facts or counting in sequences as the children move from one space to another.

Problem solving and reasoning is at the heart of all our maths lessons and throughout each unit of work we have a clear focus on language and communication, conceptual understanding and mathematical thinking. These elements are embedded within lessons so that all children have experience of problem solving and reasoning.

 

Curriculum impact:

What do our outcomes in Mathematics look like? How successful is our Mathematics teaching?

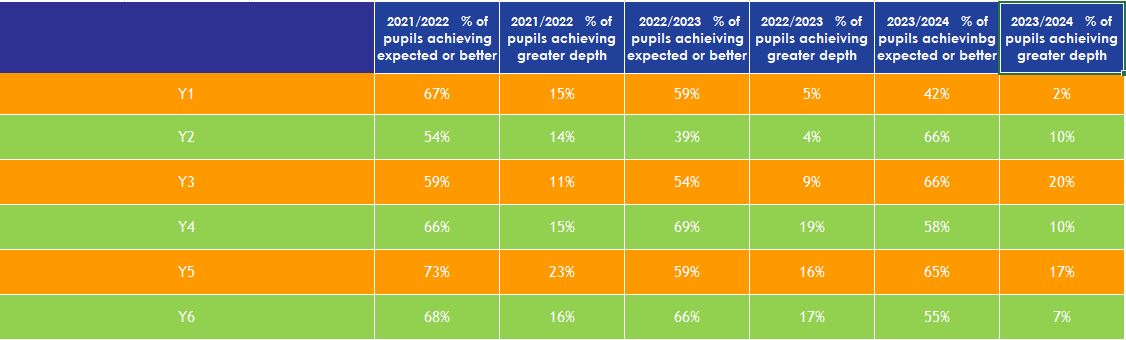
Below you will find some data from the last two years so you can see how our children are progressing in Maths. We also have some quotes from children when asked about their Maths work.